I. Introducció
L'aigua pot encendre espelmes, és veritat? És veritat!
És cert que les serps tenen por del realgar? És fals!
El que avui tractarem és:
La interferència pot millorar la precisió de la mesura, és veritat?
En circumstàncies normals, la interferència és l'enemic natural del mesurament. La interferència reduirà la precisió del mesurament. En casos greus, el mesurament no es durà a terme normalment. Des d'aquesta perspectiva, la interferència pot millorar la precisió del mesurament, cosa que és falsa!
Tanmateix, és sempre així? Hi ha alguna situació en què la interferència no redueixi la precisió de la mesura, sinó que la millori?
La resposta és sí!
2. Acord d'interferència
Combinant-ho amb la situació real, arribem al següent acord sobre la interferència:
- La interferència no conté components de corrent continu. En la mesura real, la interferència és principalment interferència de corrent altern, i aquesta suposició és raonable.
- En comparació amb el voltatge de CC mesurat, l'amplitud de la interferència és relativament petita. Això està en línia amb la situació real.
- La interferència és un senyal periòdic, o el valor mitjà és zero dins d'un període de temps fix. Aquest punt no és necessàriament cert en la mesura real. Tanmateix, com que la interferència és generalment un senyal de CA de freqüència més alta, per a la majoria d'interferències, la convenció de mitjana zero és raonable per a un període de temps més llarg.
3. Precisió de la mesura sota interferències
La majoria d'instruments de mesura i comptadors elèctrics actualment utilitzen convertidors AD, i la seva precisió de mesura està estretament relacionada amb la resolució del convertidor AD. En general, els convertidors AD amb una resolució més alta tenen una precisió de mesura més alta.
Tanmateix, la resolució de l'AD sempre és limitada. Suposant que la resolució de l'AD és de 3 bits i el voltatge de mesura més alt és de 8 V, el convertidor AD és equivalent a una escala dividida en 8 divisions, cada divisió és d'1 V. és 1 V. El resultat de la mesura d'aquest AD és sempre un nombre enter, i la part decimal sempre es porta o es descarta, cosa que se suposa que es porta en aquest document. Portar o descartar causarà errors de mesura. Per exemple, 6,3 V és més gran que 6 V i més petit que 7 V. El resultat de la mesura AD és de 7 V, i hi ha un error de 0,7 V. Anomenem aquest error error de quantificació AD.
Per facilitar l'anàlisi, suposem que l'escala (convertidor AD) no té altres errors de mesura excepte l'error de quantificació AD.
Ara, utilitzem dues escales idèntiques per mesurar els dos voltatges de corrent continu que es mostren a la Figura 1 sense interferències (situació ideal) i amb interferències.
Com es mostra a la Figura 1, el voltatge de CC real mesurat és de 6,3 V, i el voltatge de CC de la figura de l'esquerra no té cap interferència, i és un valor constant. La figura de la dreta mostra el corrent continu pertorbat pel corrent altern, i hi ha una certa fluctuació en el valor. El voltatge de CC del diagrama de la dreta és igual al voltatge de CC del diagrama de l'esquerra després d'eliminar el senyal d'interferència. El quadrat vermell de la figura representa el resultat de la conversió del convertidor AD.

Tensió de CC ideal sense interferències
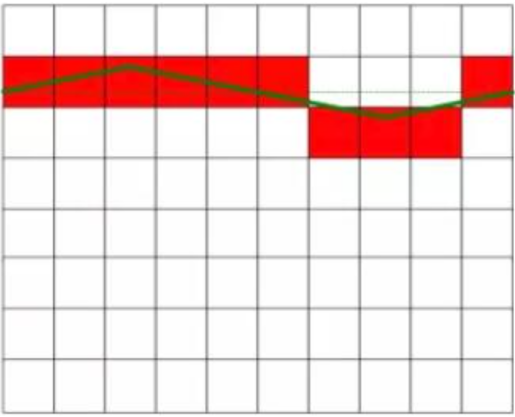
Aplicar una tensió de corrent continu interferent amb un valor mitjà de zero
Feu 10 mesures del corrent continu en els dos casos de la figura anterior i després feu la mitjana de les 10 mesures.
La primera escala de l'esquerra es mesura 10 vegades i les lectures són les mateixes cada vegada. A causa de la influència de l'error de quantificació AD, cada lectura és de 7 V. Després de fer la mitjana de 10 mesures, el resultat continua sent de 7 V. L'error de quantificació AD és de 0,7 V i l'error de mesura és de 0,7 V.
La segona escala de la dreta ha canviat dràsticament:
A causa de la diferència entre el positiu i el negatiu de la tensió d'interferència i l'amplitud, l'error de quantificació AD és diferent en diferents punts de mesura. Sota el canvi de l'error de quantificació AD, el resultat de la mesura AD canvia entre 6V i 7V. Set de les mesures van ser de 7V, només tres van ser de 6V, i la mitjana de les 10 mesures va ser de 6,3V! L'error és de 0V!
De fet, cap error és impossible, perquè en el món objectiu no hi ha un voltatge estricte de 6,3 V! Tanmateix, sí que hi ha:
En el cas que no hi hagi interferències, com que el resultat de cada mesura és el mateix, després de fer la mitjana de 10 mesures, l'error es manté sense canvis!
Quan hi ha una quantitat adequada d'interferència, després de fer la mitjana de 10 mesures, l'error de quantificació AD es redueix en un ordre de magnitud! La resolució millora en un ordre de magnitud! La precisió de la mesura també millora en un ordre de magnitud!
Les preguntes clau són:
És el mateix quan el voltatge mesurat és d'altres valors?
Els lectors poden voler seguir l'acord sobre la interferència a la segona secció, expressar la interferència amb una sèrie de valors numèrics, superposar la interferència al voltatge mesurat i després calcular els resultats de la mesura de cada punt segons el principi de carry del convertidor AD i, a continuació, calcular el valor mitjà per a la verificació, sempre que l'amplitud d'interferència pugui fer que la lectura després de la quantificació AD canviï, i la freqüència de mostreig sigui prou alta (els canvis d'amplitud d'interferència tenen un procés de transició, en lloc de dos valors positius i negatius), i cal millorar la precisió!
Es pot demostrar que sempre que el voltatge mesurat no sigui exactament un nombre enter (no existeix en el món objectiu), hi haurà un error de quantificació AD, independentment de la mida de l'error de quantificació AD, sempre que l'amplitud de la interferència sigui més gran que l'error de quantificació AD o més gran que la resolució mínima d'AD, farà que el resultat de la mesura canviï entre dos valors adjacents. Com que la interferència és simètrica positiva i negativa, la magnitud i la probabilitat de disminució i augment són iguals. Per tant, quan el valor real és més a prop de quin valor, la probabilitat que aparegui quin valor és més gran, i serà més a prop de quin valor després de fer la mitjana.
És a dir: el valor mitjà de múltiples mesures (el valor mitjà d'interferència és zero) ha d'estar més a prop del resultat de la mesura sense interferències, és a dir, utilitzar el senyal d'interferència de CA amb un valor mitjà de zero i fer la mitjana de múltiples mesures pot reduir els errors equivalents de quantificació AD, millorar la resolució de la mesura AD i millorar la precisió de la mesura!
Data de publicació: 13 de juliol de 2023




